[Look here for Part 1: Introducing Ray Kurzweil.“]
“An analysis of the history of technology shows that technological change is exponential, contrary to the common-sense “intuitive linear” view. So we won’t experience 100 years of progress in the 21st century — it will be more like 20,000 years of progress (at today’s rate).”
Ray Kurzweil March, 2001
Do you have a big lump in your back pocket, breast pocket or in your purse? Chances are you do, because each of us is carrying around a smartphone, right? This technological marvel that in many cases -barely – fits into a pocket has transformed our lives, has it not? I know it has had an impact on my life, because, based on the time I spend looking for it, I feel very lost without it! And it even repurposed the bathroom in our house by transforming it into the Instagram room! So, hell, yeah, it’s had an impact!
 So prevalent and pervasive is cell phone tech, that it’s hard to believe the first cell phone was only made 50 years ago, back in 1973. None of us knew about cell phones in the 70’s. It then took 10 more years to bring a phone to market, but when they finally did around 1984, it changed everything! A few years later, in 1997, a photo was taken with a cell phone for the first time. And again, everything changed (or at least it did for photography)! Now smartphones are counted as some of the best cameras made. For these reasons, I think the cell phone really is a great example of fast-paced technological evolution, one that is rather obvious to anyone who looks, and as such it fits my purpose here.
So prevalent and pervasive is cell phone tech, that it’s hard to believe the first cell phone was only made 50 years ago, back in 1973. None of us knew about cell phones in the 70’s. It then took 10 more years to bring a phone to market, but when they finally did around 1984, it changed everything! A few years later, in 1997, a photo was taken with a cell phone for the first time. And again, everything changed (or at least it did for photography)! Now smartphones are counted as some of the best cameras made. For these reasons, I think the cell phone really is a great example of fast-paced technological evolution, one that is rather obvious to anyone who looks, and as such it fits my purpose here.
And my purpose here is to introduce you to Ray Kurzweil’s “Law of Accelerating Returns,” which is a law that Ray uses to make his predictions, an activity for which is he is known. I won’t delve into the math more than necessary, but like many things, the math isn’t necessary to get the gist of what the law is doing. However there is something you should be aware of before dipping a toe into Ray’s law. In fact, it’s actually another law, albeit one you may have heard of before, one that Ray’s law is based on, more or less. It’s called, “Moore’s Law.”
So, what the hell is Moore’s Law?
You should know first that unlike the laws of physics, Both Moore’s Law and Ray’s law weren’t created based on nature, instead they were created based on simple observations over time. For instance, Moore’s Law was based on observing trends found on the factory floor, where transistor chips were being made.
 In the 1960’s a man named Gordon Moore, who was co-founder of both Fairchild Semiconductor and Intel (also later former CEO of Intel), was in the business of making chips with transistors. He noticed something about their production that was rather remarkable. Checking and rechecking his results, in 1964 he presented a paper with his findings titled, “The Evolving Technology of the Semiconductor Integrated Circuits” to a high-tech chip conference in San Francisco. (It’s interesting that Moore initially called it a “prediction” and not a law. He later changed it to “law” in order to highlight its empirical basis i.e., that it was based on experience and observation).
In the 1960’s a man named Gordon Moore, who was co-founder of both Fairchild Semiconductor and Intel (also later former CEO of Intel), was in the business of making chips with transistors. He noticed something about their production that was rather remarkable. Checking and rechecking his results, in 1964 he presented a paper with his findings titled, “The Evolving Technology of the Semiconductor Integrated Circuits” to a high-tech chip conference in San Francisco. (It’s interesting that Moore initially called it a “prediction” and not a law. He later changed it to “law” in order to highlight its empirical basis i.e., that it was based on experience and observation).
In this paper, Moore described and defended his claim that the number of transistors on computer chips roughly doubles every two years. (Well, actually, Moore initially said that it doubled every year, but in 1975, reanalyzing the data, he changed this to every 2 years). This then, is the crux of Moore’s Law, pure and simple: The law claims that we can expect the speed and capabilities of our computers to increase every two years because of growth, yet we will pay less for them.
For those of us who have worked in the industry, or those who have tried to keep pace with the increases in computer power every year through the 80’s and 90’s, I think we’ve all seen enough to know that Moore was really onto something with his law, because we’ve all experienced (and in some cases, profited from) this incredible growth first-hand. I should mention that Moore’s Law became the guide for the semiconductor industry for long-term planning and setting targets for R&D. In fact, “Moore’s Law has been a driving force of technological and social change, productivity, and economic growth that are hallmarks of the late 20th and early 21st centuries.”[i]
But there is another tenet in Moore’s Law that I want to call your attention to, and it’s too important to overlook. You see, Moore’s Law asserts something that Ray also asserts in his law – that such growth is not your normal, everyday type of “linear” growth. No, this growth type is “exponential.”
What does “exponential growth” mean exactly? Moore actually didn’t get into a discussion about the exponential aspect of growth much, other than declare it as an observation. But Ray Kurzweil did address it and he did so by comparing that everyday linear growth we are used to seeing, to exponential growth.
Linear growth should be very familiar. Consider a town with 100 people in it. Every year, the town adds 10 more people, a constant number of new people. In 10 years how many people does the town have? 200, right? Of course. This is linear growth:
Linear Growth
| Year | Starting Population | Annual Increase | Ending Population |
| 1 | 100 | 10 | 110 |
| 2 | 110 | 10 | 120 |
| 3 | 120 | 10 | 130 |
| 4 | 130 | 10 | 140 |
| . | |||
| . | |||
| ‘ | |||
| 10 | 190 | 10 | 200 |
Exponential growth is something different – something else. Definitely not linear! Linear growth means that something grows by a constant amount for each unit of time. In my example above, we add 10 people every year as our constant amount.
With exponential growth, you’re watching something grow over time at an accelerating rate.
Note that with linear growth (table above) we are adding a constant value to our total. In this case, 10 people per month. But with exponential growth (table below), we’re no longer adding a constant 10 people per year. Instead we’re increasing the annual growth rate by a constant percentage (10% growth increase per year) and we’re assuming the rate stays consistent every year.
| Year | Starting Population | % annual Increase | Ending Population |
| 1 | 100 | 10% | 110 |
| 2 | 110 | 10% | 121 |
| 3 | 121 | 10% | 133 |
| 4 | 133 | 10% | 146 |
| . | |||
| . | |||
| ‘ | |||
| 10 | 235 | 10% | 259 |
See the difference between linear and exponential?
Sure you do. In the linear growth example above, 10 years of growth with a constant 10 people being added every year resulted in a population of 200 people. But the exponential growth over the same time period of 10 years, this time with a constant population rate increase of 10% resulted in 259 people. Exponential growth is more, as it shows 113 more people than the linear growth table.
Wow! Right? Well, okay, maybe not wow. It’s not that much more, is it? A bit disappointing, I had to admit.
To be honest, I expected to see a more dramatic increase and perhaps you did, too? Well, there is a reason we don’t see the drama with this example. This is because with only a 10-year time period and a 10% population rate increase per year, the difference between linear and exponential growth is not going to look all that different. In fact with this short of a time period and this low of a rate increase, it’s almost a straight line, actually, if you were to graph it out. This is because of the small base population which makes the initial growth seem somewhat similar.
However, when you extend the time period and make it longer, the difference between linear and exponential becomes much more apparent.
Take a look:
| Year | Linear Total | Exponential Total |
| 10 | 200 | 259 |
| 20 | 300 | 673 |
| 50 | 600 | 11,739 |
Whoa! Now we’re talking! While you might have looked at the first 10 years of data and wondered whether the change was meaningful or not, suddenly the rate difference is noticeable! But that is a deceptive perception! And from there the rate just continues to climb, to skyrocket. Maybe now you can see why exponential growth is much more than linear growth.
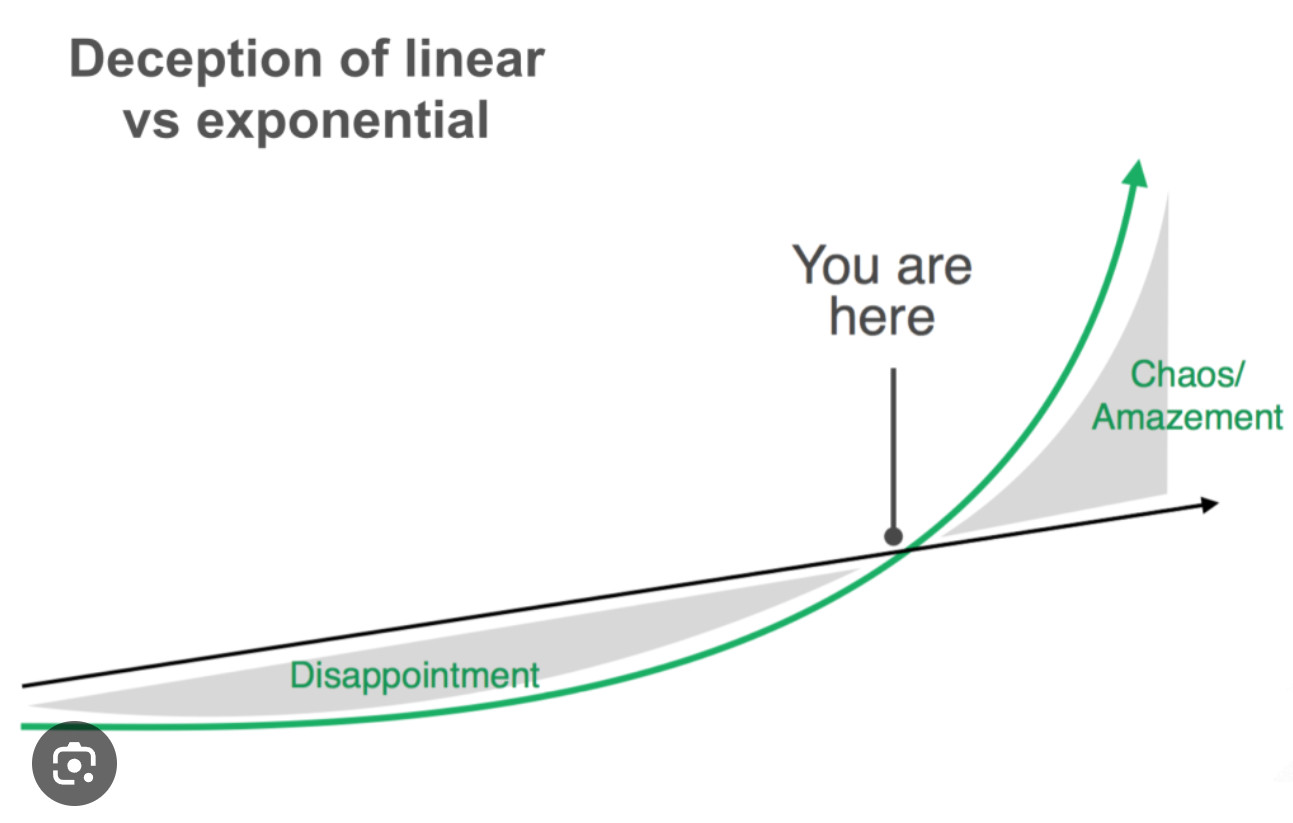 My focus in this blog post is exponential growth, so I’m not going to say much more about linear growth, other than I think Ray was right to call linear growth out as “intuitive” and something we all can recognize in our lives. The bottom line is that Ray believed the Linear Growth model was a limited tool and was unsuitable for modeling new “transformative” technologies. Ray didn’t believe that linear growth could explain the rapid advancements observed in fields like technology, AI, and biotechnology. Ray argues that these fields are distinct by their exponential growth rates, not linear.
My focus in this blog post is exponential growth, so I’m not going to say much more about linear growth, other than I think Ray was right to call linear growth out as “intuitive” and something we all can recognize in our lives. The bottom line is that Ray believed the Linear Growth model was a limited tool and was unsuitable for modeling new “transformative” technologies. Ray didn’t believe that linear growth could explain the rapid advancements observed in fields like technology, AI, and biotechnology. Ray argues that these fields are distinct by their exponential growth rates, not linear.
Okay, so that’s kind of cool. But why did Ray think that fields like technology, AI, biotech, etc. experienced exponential growth as opposed to some others? His reasoning included a few key points:
Positive Feedback Loops
Familiar with positive feedback loops? You are. We use them all the time, although you may not realize it. Put simply, a feedback loop happens when a change in something causes a further change in the same thing.
For example, in business a feedback loop is created when customer or employee feedback on say, a product, is used to improve that product. In other words, some portion of the system’s output (in this case, likes or dislikes of product features reported by customers) is then turned around and used as input for future operations (in this case, product improvements).
As you might guess, if there is a positive feedback loop, there is also a negative feedback loop! Positive feedback loops cause changes to occur in the same direction. Negative feedback loops cause changes to go in the opposite direction. A negative feedback loop for a business product could consist of customer product complaints being ignored leading customers to become dissatisfied with a product, which in turn causes a reduction in sales, which in turn leads to layoffs, etc. You get the picture. Positive good, negative bad.
Looking at the history of technology, Ray believed that technological advances often created positive feedback loops, where each new breakthrough enabled further progress at an accelerated rate. For example, the development of more powerful computers led to the development of more powerful algorithms, which led to even more powerful computers. He believed, and rightly so, I think, that this self-reinforcing cycle can drive exponential growth.
Non-linear Effects
A non-linear effect is when a small change leads to some major, or large scale transformation, probably something no one saw coming. For example, the invention of the transistor completely transformed the electronics industry, and later the world. A transistor is simply a semiconductor device that can amplify or switch electrical signals. The geezers among us might remember huge living room radios filled with tubes, and of course, TVs with their tubes, too. I also remember getting my first transistor radio, which barely fit in the palm of my hand. The difference between them was the transistor. Super small. Tiny. This led to the miniaturization of electronics, which in turn led to computers, the internet, the list goes on and on! Non-linear effects can cause technological progress to increase rapidly. No one saw this change coming, except Ray. He saw the internet we know today coming way before anyone else did.
Increasing Returns to Scale
As technologies mature, they often exhibit something called “increasing returns to scale,” meaning that the cost of producing additional units decreases as the scale of production increases. This can make it much cheaper and easier to develop new technologies, further accelerating the pace of technological progress.
The Power of Moore’s Law
Moore’s Law (discussed above) states that the number of transistors on a microchip doubles roughly every two years. This exponential growth in computing power has been a major driver of technological progress in recent decades, and Kurzweil believes it is likely to continue for many years to come.
The Convergence of Technologies
Technologies can sometimes converge knowingly or even unknowingly, creating new and often unforeseen possibilities. This can often lead to breakthroughs that would not have been possible had the technologies remained separate, leading again to accelerated growth. Examples that spring to mind are the smartphone: using it to not only talk, but also take photos, play music, games, etc. The smart TV, where it is not only used to watch TV shows, but is also used to surf the internet. Smart watches. Drones. You get the point. I am anxious to see what happens when an AI will be focused on nanotechnology!
So, this is some of the key thoughts that Ray Kurzweil used to develop his Law of Accelerating Returns. Please be aware that Ray has his detractors! His critics argue that there are physical and logical limits to technological progress and that the pace of growth will eventually slow down. I find it hard to argue with his critics on this, except to say that I don’t think we’re there yet. And until things start really slowing down for technologies, his law seems to continue making sense to me.
My next blog post will dive into Ray Kurzweil’s predictions!
[i] Investopedia.
[…] Look here for Part 1: Introducing Ray Kurzweil and Part 2: The Law of Accelerating Returns (Explained) and Part 3: Ray Kurzweil’s Six Epochs of my series on Ray […]
[…] In Part 2 of my series about Ray, I will go through some of his predictions and also explain this thing he calls, “The Law of Accelerating Returns.” […]
[…] Look here for Part 1: Introducing Ray Kurzweil and Part 2: The Law of Accelerating Returns (Explained) of my series on Ray […]